在数列 中,
中,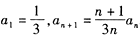
(1)证明 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)求 的前n项和
的前n项和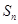
已知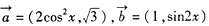 ,函数
,函数
(1)求方程g(x)=0的解集;
(2)求函数f(x)的最小正周期及其单调增区
在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为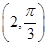 .
.
(1)求圆C的极坐标方程;
(2)P是圆C上一动点,点Q满足3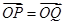 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos 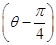 =2
=2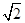 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
(1)设x≥1,y≥1,证明x+y+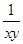 ≤
≤ +
+ +xy;
+xy;
(2)1<a≤b≤c,证明logab+logbc+logca≤logba+logcb+logac.