已知直线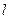 的参数方程:
的参数方程: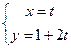 (
(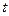 为参数)和圆
为参数)和圆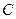 的极坐标方程:
的极坐标方程: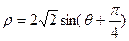 .
.
(Ⅰ)将直线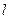 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆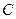 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)判断直线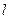 和圆
和圆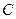 的位置关系.
的位置关系.
(本小题满分12分)
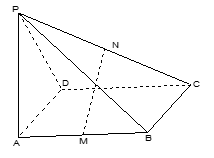
如图,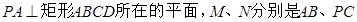 的中点.
的中点.
(1)求证: ;(2)求证:
;(2)求证: ;
; 
(本小题满分12分)
对某校高二年级学生参加社区服务次数进行统计,随机抽取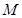 名学生作为样本,得到这
名学生作为样本,得到这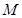 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率 分布直方图如下:
分布直方图如下: 
| 分组 |
频数 |
频率 |
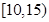 |
10 |
0.25 |
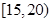 |
24 |
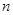 |
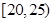 |
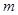 |
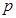 |
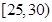 |
2 |
0.05 |
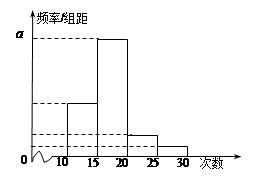
| 合计 |
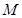 |
1 |
(1)求出表中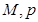 及图中
及图中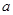 的值;
的值;
(2)若该校高二学生有240人,试估计该校高二学生参加社区服务的次数在区间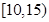 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间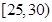 内的概率.
内的概率.
.(本小题满分12分)
已知函数
(1)求函数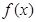 的最大值和最小正周期;
的最大值和最小正周期;
(2)设 的内角
的内角
 的对边分别
的对边分别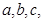 且
且 ,
, ,若
,若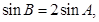 求
求 的值.
的值.
(本小题满分13分)
已知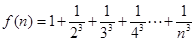 ,
, ,
,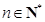 .
.
(1)当 时,试比较
时,试比较 与
与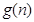 的大小关系;
的大小关系;
(2)猜想 与
与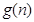 的大小关系,并给出证明.
的大小关系,并给出证明.
13分)已知函数
(1)求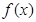 的单调区间;
的单调区间;
(2)设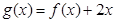 ,若
,若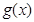 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.