设函数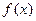
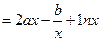
(Ⅰ)若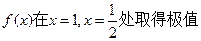 ,
,
( i )求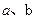 的值;
的值;
( ii)在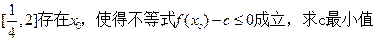 ;
;
(Ⅱ)当
 上是单调函数,求
上是单调函数,求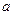 的取值范围。
的取值范围。
(参考数据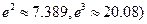
(本小题满分12分)
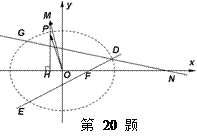
如图,点 是椭圆
是椭圆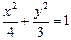 上一动点,点
上一动点,点 是点
是点 在
在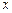 轴上的射影,坐标平面
轴上的射影,坐标平面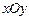 内动点
内动点 满足:
满足: (
(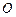 为坐标原点),设动点
为坐标原点),设动点 的轨迹为曲线
的轨迹为曲线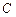 .
.
(Ⅰ)求曲线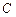 的方程并画出草图;
的方程并画出草图;
(Ⅱ)过右焦点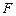 的直线
的直线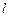 交曲线
交曲线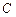 于
于 ,
, 两点,且
两点,且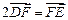 ,点
,点 关于
关于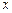 轴的对称点为
轴的对称点为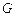 ,求直线
,求直线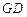 的方程.
的方程.
(本小题满分12分)
如图,四棱锥 的底面
的底面 为菱形,
为菱形, 平面
平面 ,
,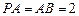 ,
, 分别为
分别为 的中点,
的中点, .
.
(Ⅰ)求证: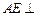 平面
平面 .
.
(Ⅱ)求三棱锥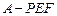 的体积.
的体积.
本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组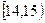 ……第五组
……第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知
求事件“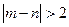 ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 |
男 |
女 |
合计 |
| 达标 |
 |
 ______ ______ |
_____ |
| 不达标 |
 _____ _____ |
 |
_____ |
| 合计 |
______ |
______ |
 |
根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
(本小题满分12分)
已知在 中,角
中,角 ,
, ,
, 的对边的边长分别为
的对边的边长分别为 ,
, ,
, ,且
,且
 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)现给出三个条件:① ;②
;② ;③
;③ .
.
试从中选出两个可以确定 的条件,写出你的选择,并以此为依据求出
的条件,写出你的选择,并以此为依据求出
 的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
(本小题满分12分)
已知点Pn(an,bn)都在直线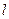 :y=2x+2上,P1为直线
:y=2x+2上,P1为直线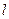 与x轴的交点,数列
与x轴的交点,数列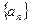 成等差数列,公差为1.(n∈N+)
成等差数列,公差为1.(n∈N+)
(1)求数列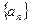 ,
,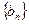 的通项公式;
的通项公式;
(2)若f(n)=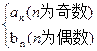 问是否存在k
问是否存在k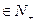 ,使得f(k+5)=2f(k)-2成立;若存在,求出
,使得f(k+5)=2f(k)-2成立;若存在,求出 k的值,若不存在,说明理由。
k的值,若不存在,说明理由。
(3)求证: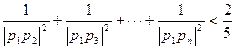 (n≥2,n∈N+)
(n≥2,n∈N+)