(本小题满分13分)已知椭圆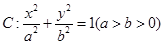 的左、右焦点分别为
的左、右焦点分别为 ,椭圆上的点
,椭圆上的点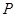 满足
满足 ,且
,且 的面积为
的面积为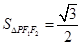 .
.
(1)求椭圆C的方程;
(2)设椭圆 的左、右顶点分别为
的左、右顶点分别为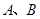 ,过点
,过点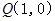 的动直线
的动直线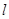 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线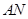 与直线
与直线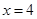 的交点为
的交点为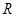 ,证明:点
,证明:点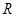 总在直线
总在直线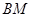 上.
上.
设函数
(1)求 的值;(2)若
的值;(2)若 ,求
,求
已知集合 ,集合
,集合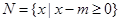 .
.
(1) 若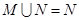 ,求实数
,求实数 的取值范围;
的取值范围;
(2) 若 ,求实数
,求实数 的取值范围.
的取值范围.
化简求值:(1)已知 ,求
,求 ;
;
(2)  .
.
两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.
求:1)d的变化范围;
2)当d取最大值时两条直线的方程.

本公司计划2012年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?