由经验得知,在某商场付款处排队等候付款的人数及概率如下表
| 排队人数 |
0 |
1 |
2 |
3 |
4 |
5人以上 |
| 概率 |
0.1 |
0.16 |
0.3 |
0.3 |
0.1 |
0.04 |
(1)至多有2人排队的概率是多少?
(2)至少有2人排队的概率是多少?
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
5 |
||
| 女生 |
10 |
||
| 合计 |
50 |
已右在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为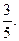
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(Ⅲ)已知喜爱打篮球的10位女生中,A1,A2,A3,A4,A5还喜欢打羽毛球,B1,B2,B3还喜欢打乒乓球,C1,C2还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率。
下面的临界值表供参考:
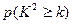 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| P |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: 其中
其中 )
)
((本小题满分12分)在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2, ,E、F分别是BA、BC的中点,G是AA1上一点,且
,E、F分别是BA、BC的中点,G是AA1上一点,且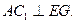
(Ⅰ)确定点G的位置;
(Ⅱ)求三棱锥C1—EFG的体积.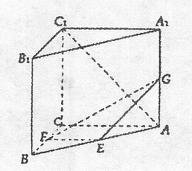
(本小题满分12分)已知数列 为等差数列,且
为等差数列,且 为等比数列,数列
为等比数列,数列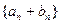 的前三项依次为3,7,13。求
的前三项依次为3,7,13。求
(Ⅰ)数列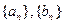 的通项公式;
的通项公式;
(Ⅱ)数列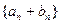 的前
的前 项和
项和
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
在三棱锥ABCD中,平面DBC⊥平面ABC,△ABC为正三角形, AC=2,DC=DB= ,
,
(1)求DC与AB所成角的余弦值;
(2)在平面ABD上求一点P,使得CP⊥平面AB D. 
必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
某商场搞促销,当顾客购买商品的金额达到一定数量之后可以抽奖,根据顾客购买商品的金额,从箱中(装有4只红球,3只白球,且除颜色外,球的外部特征完全相同)每抽到一只红球奖励20元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中)
(1)当顾客购买金额超过500元而少于1000元(含1000元)时,可从箱中一次随机抽取3个小红球,求其中至少有一个红球的概率;
(2)当顾客购买金额超过1000元时,可一次随机抽取4个小球,设他所获奖商品的金额为 元,求
元,求 的概率分布列和数学期望.
的概率分布列和数学期望.