(本题满分14分)
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视
观众,相关的数据如下表所示:
| |
文艺节目 |
新闻节目 |
总计 |
| 20至40岁 |
40 |
18 |
58 |
| 大于40岁 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
(1) 由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2) 用分层抽样方法在收看新闻节目的观众中随机抽出5名,大于40岁的观众应该
抽取几名?
(3) 在上述抽取的5名观众中任取出2名,求恰有1名观众年龄20岁至40岁的概率。
已知函数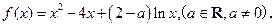
(1)当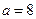 时,求函数
时,求函数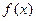 的单调区间;
的单调区间;
(2)求函数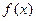 在区间
在区间 上的最小值.
上的最小值.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 作直线
作直线 交
交 于
于 、
、 两点,试问:在
两点,试问:在 轴上是否存在一个定点
轴上是否存在一个定点 ,使
,使 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知直角梯形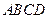 中,
中, ,
,
 过
过 作
作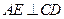 ,垂足为
,垂足为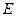 ,
,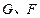 分别为
分别为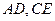 的中点,现将
的中点,现将 沿
沿 折叠使二面角
折叠使二面角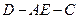 的平面角的正切值为
的平面角的正切值为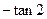 .
.
(1)求证: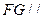 平面
平面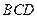 ;
;
(2)求异面直线 与
与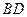 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角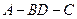 的大小.
的大小.
已知函数 ,数列
,数列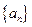 满足
满足 ,
,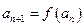 ,
, .
.
(1)求证: ;
;
(2)求证: 是递减数列;
是递减数列;
(3)设 的前
的前 项和为
项和为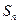 ,
,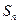 与
与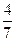 是否有确定的大小关系,如果有给出证明,如果没有给出反例.
是否有确定的大小关系,如果有给出证明,如果没有给出反例.
某校设计了一个实验学科的实验考查方案:考生从 道备选题中一次性随机抽取
道备选题中一次性随机抽取 题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中
题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中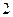 题的便可通过考查.已知
题的便可通过考查.已知 道备选题中考生甲有
道备选题中考生甲有 题能正确完成,
题能正确完成,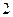 题不能完成;考生乙每题正确完成的概率都是
题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响. 求:
,且每题正确完成与否互不影响. 求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.