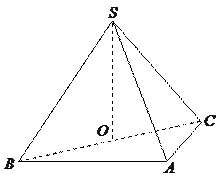如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, 为
为 中点,作
中点,作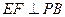 交
交 于
于

(1)求PF:FB的值
(2)求平面 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。
(本小题满分12分)将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率.
(本小题满分14分)
如图,直线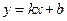 与椭圆
与椭圆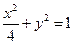 交于
交于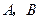 两点,记
两点,记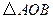 的面积为
的面积为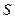 .
.
(I)求在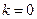 ,
,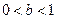 的条件下,
的条件下,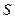 的最大值;
的最大值;
(II)当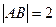 ,
,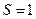 时,求直线
时,求直线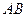 的方程.
的方程.
(本小题满分14分)
已知数列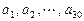 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为 的等差数列;
的等差数列;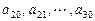 是公差为
是公差为 的等差数列(
的等差数列( ).
).
(1)若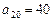 ,求
,求 ;
;
(2)试写出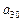 关于
关于 的关系式,并求
的关系式,并求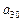 的取值范围;
的取值范围;
(3)续写已知数列,使得 是公差为
是公差为 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
(本小题满分14分)
设函数 R.
R.
(1)若 处取得极值,求常数
处取得极值,求常数 的值;
的值;
(2)若 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.
(本小题满分14分)
如图,在三棱锥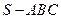 中,侧面
中,侧面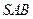 与侧面
与侧面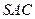 均为等边三角形,
均为等边三角形,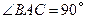 ,
,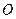 为
为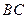 中点.
中点.
(1)证明: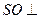 平面
平面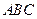 ;
;
(2)求二面角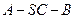 的余弦值.
的余弦值.