(本小题满分14分)
已知数列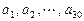 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为 的等差数列;
的等差数列;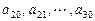 是公差为
是公差为 的等差数列(
的等差数列( ).
).
(1)若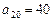 ,求
,求 ;
;
(2)试写出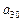 关于
关于 的关系式,并求
的关系式,并求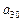 的取值范围;
的取值范围;
(3)续写已知数列,使得 是公差为
是公差为 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) |
0 |
1 |
2 |
3 |
| 频数 |
1 |
5 |
9 |
5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(1)求当天商品不进货的概率;
(2)记
为第二天开始营业时该商品的件数,求
的分布列和数学期望。
在
中,角
所对的边分别为
,且满足
.
(1)求角
的大小;
(2)求
的最大值,并求取得最大值时角
的大小.
已知函数 (a是常数,a∈R)
(a是常数,a∈R)
(1)当a=1时求不等式 的解集.
的解集.
(2)如果函数 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.
已知曲线 (
( 为参数),曲线
为参数),曲线 ,将
,将 的横坐标伸长为原来的2倍,纵坐标缩短为原来的
的横坐标伸长为原来的2倍,纵坐标缩短为原来的 得到曲线
得到曲线 .
.
(1)求曲线 的普通方程,曲线
的普通方程,曲线 的直角坐标方程;
的直角坐标方程;
(2)若点P为曲线 上的任意一点,Q为曲线
上的任意一点,Q为曲线 上的任意一点,求线段
上的任意一点,求线段 的最小值,并求此时的P的坐标.
的最小值,并求此时的P的坐标.
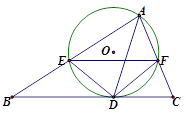
如图,在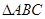 中,
中,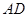 是的∠A的平分线,圆
是的∠A的平分线,圆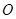 经过点
经过点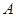 与
与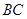 切于点
切于点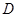 ,与
,与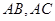 相交于
相交于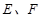 ,连结
,连结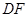 ,
,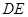 .
.
(1)求证: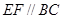 ;(2)求证:
;(2)求证: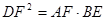 .
.