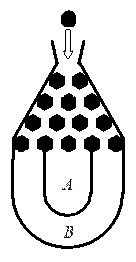
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是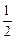 .
.
(Ⅰ)求小球落入 袋中的概率
袋中的概率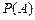 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记 为落入
为落入 袋中的小球个数,试求
袋中的小球个数,试求 的概率和
的概率和 的数学期望
的数学期望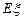 .
.
(本小题满分12分) 已知函数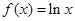 .
.
(1)求函数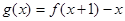 的最大值;
的最大值;
(2)求证: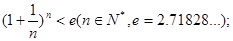
(3)当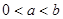 时,求证:
时,求证: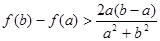 .
.
(本小题满分12分)过椭圆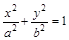 的右焦点
的右焦点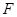 作斜率
作斜率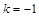 的直线交椭圆于
的直线交椭圆于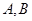 两点,且
两点,且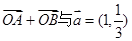 共线.
共线.
(1)求椭圆的离心率;
(2)当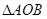 的面积
的面积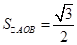 时,求椭圆的方程.
时,求椭圆的方程.
(本小题满分12分)如图,三棱柱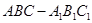 中,平面
中,平面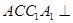 平面
平面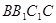 ,四边形
,四边形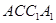 是矩形,
是矩形,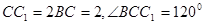 ,
,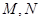 分别为
分别为 的中点.
的中点.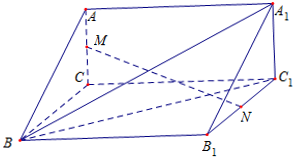
(1)求证: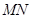 ∥平面
∥平面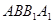 ;
;
(2)求点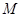 到平面
到平面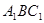 的距离
的距离 .
.
(本小题满分12分)为了促进学生的全面发展,贵州省某中学重视学生社团文化建设,现用分层抽样的方法从“海济社”,“话剧社”,“动漫社”,“彩虹文艺社”四个社团中抽取若干人组成社团管理小组,有关数据见下表(单位:人):
| 社团 |
相关人数 |
抽取人数 |
| 海济社 |
140 |
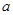 |
| 话剧社 |
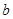 |
1 |
| 动漫社 |
105 |
3 |
| 彩虹文艺社 |
70 |
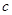 |
(1)求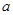 ,
,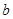 ,
,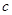 的值;
的值;
(2)若从“海济社”,“彩虹文艺社”社团已抽取的人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
(本小题满分12分) 在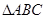 中,角
中,角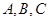 的对边分别为
的对边分别为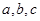 ,向量
,向量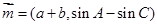 ,向量
,向量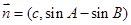 ,且
,且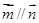 ;
;
(Ⅰ)求角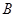 的大小;
的大小;
(Ⅱ)设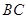 中点为
中点为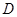 ,且
,且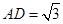 ;求
;求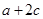 的最大值及此时
的最大值及此时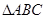 的面积。
的面积。