(本小题满分10分)
某班从4名男同学和2名女同学中任选3人参加全校举行的“八荣八耻”教育演讲赛。如果设随机变量 表示所选3人中女同学的人数.
表示所选3人中女同学的人数.
(1)若 ,求共有不同选法的种数;
,求共有不同选法的种数;
(2)求 的分布列和数学期望;
的分布列和数学期望;
(3)求“ ”的概率.
”的概率.
在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
已知命题 “椭圆
“椭圆 的焦点在
的焦点在 轴上”;
轴上”;
命题 在
在 上单调递增,若“
上单调递增,若“ ”为假,求
”为假,求 的取值范围.
的取值范围.
如图,已知直线 (
( )与抛物线
)与抛物线 :
: 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求 与
与 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以 、
、 为邻边作平行四边形
为邻边作平行四边形 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 ,直线
,直线 与
与 轴交点为
轴交点为 ,连接
,连接 交抛物线
交抛物线 于
于 、
、 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
已知函数
(Ⅰ)若函数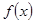 恰好有两个不同的零点,求
恰好有两个不同的零点,求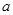 的值。
的值。
(Ⅱ)若函数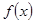 的图象与直线
的图象与直线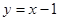 相切,求
相切,求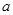 的值及相应的切点坐标。
的值及相应的切点坐标。
已知 ,
,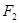 是椭圆
是椭圆
 左右焦点,它的离心率
左右焦点,它的离心率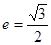 ,且被直线
,且被直线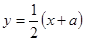 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设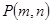 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求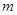 的取值范围。
的取值范围。