对于函数 ,若存在实数
,若存在实数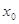 ,使
,使 成立,则称
成立,则称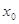 为
为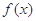 的不动点.
的不动点.
⑴当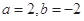 时,求
时,求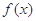 的不动点;
的不动点;
⑵若对于任何实数 ,函数
,函数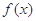 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数 的取值范围;
的取值范围;
⑶在⑵的条件下,若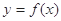 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数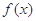 的不动点,且直线
的不动点,且直线 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
等比数列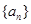 的前
的前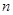 项和为
项和为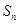 ,公比
,公比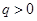 ,已知
,已知 .
.
(1)求数列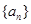 的通项公式;
的通项公式;
(2)若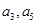 分别为等差数列
分别为等差数列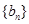 的第4项和第16项,试求数列
的第4项和第16项,试求数列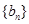 的通项公式及前
的通项公式及前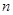 项和
项和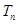 .
.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.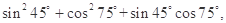
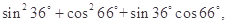
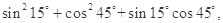
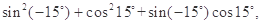
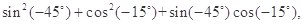
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
已知关于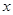 的不等式
的不等式 的解集为
的解集为 .
.
(1)求实数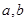 的值;
的值;
(2)解关于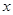 的不等式:
的不等式: (
( 为常数).
为常数).
在△ABC中,角A,B,C所对的边分别为 ,设S为△ABC的面积,且
,设S为△ABC的面积,且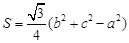 。
。
(Ⅰ)求角A的大小;
(Ⅱ)若 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
等比数列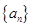 的各项均为正数,且
的各项均为正数,且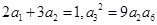 .
.
(1)求数列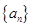 的通项公式;
的通项公式;
(2)设  ,求数列
,求数列 的前
的前 项和
项和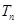 .
.