已知椭圆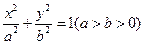 的离心率为
的离心率为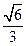 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为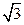 ,直线
,直线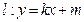 交椭圆于不同的两点
交椭圆于不同的两点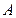 ,
,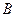
(Ⅰ)求椭圆的方程
(Ⅱ)若坐标原点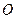 到直线
到直线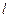 的距离为
的距离为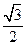 ,求
,求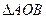 面积的最大值
面积的最大值
如图①,正三角形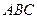 边长2,
边长2,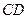 为
为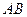 边上的高,
边上的高,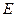 、
、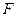 分别为
分别为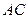 、
、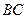 中点,现将
中点,现将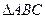 沿
沿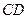 翻折成直二面角
翻折成直二面角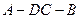 ,如图②
,如图②
(1)判断翻折后直线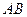 与面
与面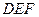 的位置关系,并说明理由
的位置关系,并说明理由
(2)求二面角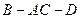 的余弦值
的余弦值
(3)求点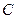 到面
到面 的距离
的距离
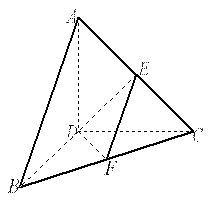
图 ①图 2
在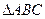 中,
中,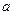 、
、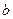 、
、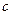 为角
为角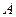 、
、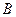 、
、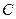 的对边,已知
的对边,已知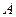 、
、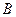 为锐角,且
为锐角,且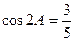 ,
,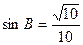
(1)求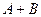 的值
的值
(2)若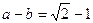 ,求
,求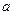 、
、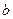 、
、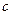 的值
的值
某车间甲组10名工人,其中4名女工人,乙组5名工人,其中3名女工人,现采用分层抽样方法,从甲乙两组中共抽取3名工人进行技术考核
(1)求从甲乙两组各抽取的人数
(2)求从甲组抽取的2人中恰有1名女工的概率
(3)用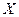 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求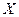 的分布列及数学期望
的分布列及数学期望
设函数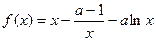
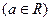 .
.
(I)若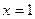 是函数
是函数
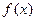 的极大值点,求
的极大值点,求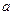 的取值范围;
的取值范围;
(II)当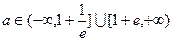 时,若在
时,若在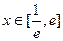 上至少存在一点
上至少存在一点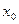 ,使
,使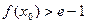 成立,求
成立,求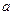 的取值范围.
的取值范围.