某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.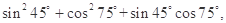
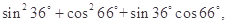
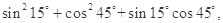
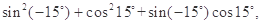
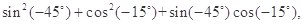
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 |
 |
 |
 |
 |
 |
 |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生“智力评分”频数分布表
| 智力评分 |
 |
 |
 |
 |
 |
 |
| 频数 |
1 |
7 |
12 |
6 |
3 |
1 |
(1)求高一的男生人数并完成下面男生的频率分布直方图;
(2)估计该校学生“智力评分”在[1 65,1 80)之间的概率;
(3)从样本中“智力评分”在[180,190)的男生中任选2人,求至少有1人“智力评分”在[185,190)之间的概率.
(本小题满分12分)在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
(1)求角 的值;
的值;
(2)若 且
且 ,求
,求 的取值范围.
的取值范围.
设函数 .
.
(1)若函数 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值;
(2)若存在 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,已知椭圆 ,直线
,直线 的方程为
的方程为 ,过右焦点
,过右焦点 的直线
的直线 与椭圆交于异于左顶点
与椭圆交于异于左顶点 的
的 两点,直线
两点,直线 ,
, 交直线
交直线 分别于点
分别于点 ,
, .
.
(1)当 时,求此时直线
时,求此时直线 的方程;
的方程;
(2)试问 ,
, 两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.
两点的纵坐标之积是否为定值?若是,求出该定值;若不是,请说明理由.
设数列 为等差数列,且
为等差数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且 .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若 ,
, 为数列
为数列 的前
的前 项和,
项和, 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.