为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 |
 |
 |
 |
 |
 |
 |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生“智力评分”频数分布表
| 智力评分 |
 |
 |
 |
 |
 |
 |
| 频数 |
1 |
7 |
12 |
6 |
3 |
1 |
(1)求高一的男生人数并完成下面男生的频率分布直方图;
(2)估计该校学生“智力评分”在[1 65,1 80)之间的概率;
(3)从样本中“智力评分”在[180,190)的男生中任选2人,求至少有1人“智力评分”在[185,190)之间的概率.
某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5,(相互独立)
(1)求至少3人同时上网的概率
(2)至少几人同时上网的概率小于0.3?
成等差数列的三个正数的和等于15,并且这三个数分别加上1,3,9之后又成等比数列,求这三个数。
如图,Rt△ABC中,AC=BC=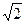 ,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。
,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。
 C. C
C. C  D
D
A. D. B. A. B
计算(每题 6分,共18分)
(1)2log525 + 3log264(2)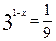 (3)
(3)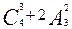 =
=
.(本小题满分14分)
已知等比数列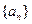 的前
的前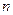 项和
项和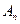 =
=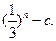 数列
数列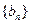
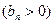 的首项为
的首项为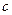 ,且前
,且前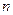 项和
项和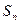 满足
满足 -
-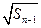 =1(
=1(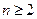 .)
.)
(1)求数列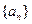 的通项公式
的通项公式
(2)求数列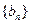 的通项公式
的通项公式
(3)若数列{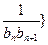 前
前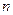 项和为
项和为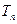 ,问
,问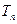 >
>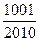 的最小正整数
的最小正整数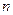 是多少?
是多少?