（本小题满分13分）
已知椭圆
：
上的一动点
到右焦点的最短距离为
，且右焦点到右准线的距离等于短半轴的长．
(Ⅰ) 求椭圆的方程；
(Ⅱ) 过点
(
，
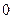)的动直线
交椭圆于
、
两点，试问：在坐标平面上是否存在一个定点
，使得无论如何转动，以为直径的圆恒过定点？若存在，求出点的坐标；若不存在，请说明理由．
已知向量a=（4，5cosσ），b=（3，-4tanσ），
（1）若a//b，试求sinσ的值。
（2）若a⊥b，且σ∈（0，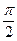
），求cos（2σ-
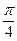）的值
（（本小题满分12分）
已知圆C：x2+(y－1)2 =5，直线l：mx－y+l－m=0，
（1）求证：对任意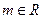
，直线l与圆C总有两个不同的交点。
（2）设l与圆C交于A、B两点，若| AB | =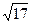 
，求l的倾斜角；
（3）求弦AB的中点M的轨迹方程；
（（本小题满分12分）
某学校准备购买一批电脑，在购买前进行的市场调查显示：在相同品牌、质量与售后服务的条件下，甲、乙两公司的报价都是每台6000元。甲公司的优惠条件是购买10台以上的，从第11台开始按报价的七折计算，乙公司的优惠条件是均按八五折计算。
（1）分别写出在两公司购买电脑的总费用y甲、y乙与购买台数x之间的函数关系式；
（2
）根据购买的台数，你认为学校应选择哪家公司更合算？说明理由。
（（本小题满分12分）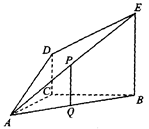
如图，DC⊥平面ABC，EB // DC，AC =BC = EB = 2DC=2，∠ACB＝120°，
P，Q分别为AE，AB的中点。
(1)证明：PQ //平面ACD；
(2)求AD与平面ABE所成角的正弦值。
（（本小题满分12分）
已知点P（x，y）在圆x2+y2－6x－6y+14=0上。
（1）求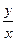
的最大值和最小值；
（2）求x2+y2+2x+3的最大值与最小值；