(本小题满分15分)
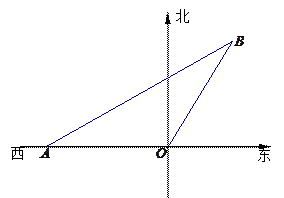
如图,我市现有自市中心 通往正西和东偏北
通往正西和东偏北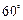 方向的两条公路.为了解决市区交通拥挤问题,市政府决定修建一条环城公路,分别在通往正西和东偏北
方向的两条公路.为了解决市区交通拥挤问题,市政府决定修建一条环城公路,分别在通往正西和东偏北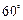 方向的两条公路上选取
方向的两条公路上选取 两点,环城公路为
两点,环城公路为 间的直线段,设计要求市中心
间的直线段,设计要求市中心 到
到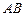 段的距离为10km,且
段的距离为10km,且 间的距离最小,请你确定
间的距离最小,请你确定 两点的位置
两点的位置
 |
已知 ,向量 是矩阵 的属性特征值 的一个特征向量,求矩阵 以及它的另一个特征值.
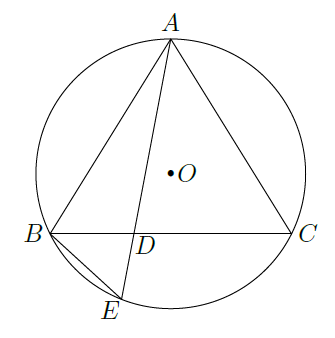
如图,在 中, , 的外接圆圆 的弦 交 于点D.
求证: .
设
是各项为正数且公差为d
的等差数列
(1)证明:
依次成等比数列;
(2)是否存在
,使得
依次成等比数列,并说明理由;
(3)是否存在
及正整数 ,使得
依次成等比数列,并说明理由.
,使得
依次成等比数列,并说明理由.
已知函数
.
(1)试讨论
的单调性;
(2)若
(实数
是
与无关的常数),当函数
有三个不同的零点时,
的取值范围恰好是
,求
的值.
如图,在平面直角坐标系
中,已知椭圆
的离心率为
,且右焦点
到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过
的直线与椭圆交于
两点,线段
的垂直平分线分别交直线
和
于点
,若
,求直线
的方程.