(本小题满分12分)
已知函数 和函数
和函数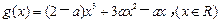
(Ⅰ)令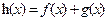 ,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
(Ⅱ)当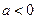 时,若
时,若 有极大值-7,求实数
有极大值-7,求实数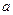 的值.
的值.
已知 中,
中, 求:(1)边b的长;(2)求
求:(1)边b的长;(2)求 的面积。
的面积。
已知向量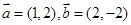
(1)设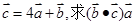 ;(2)若
;(2)若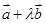 与
与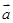 垂直,求
垂直,求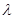 的值.
的值.
已知函数 在
在 处取得极值,
处取得极值,
(1)求实数 的值;
的值;
(2)若关于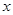 的方程
的方程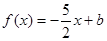 在区间
在区间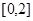 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数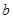 的取值范围.
的取值范围.
已知函数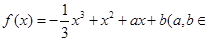
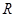 ).
).
(Ⅰ) 若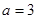 ,试确定函数
,试确定函数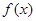 的单调区间;
的单调区间;
(Ⅱ) 若函数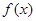 在其图象上任意一点
在其图象上任意一点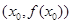 处切线的斜率都小于
处切线的斜率都小于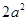 ,求实数
,求实数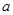 的取值范围.
的取值范围.
经调查某校高三年级学生家庭月平均收入不多于10000元的共有1000人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.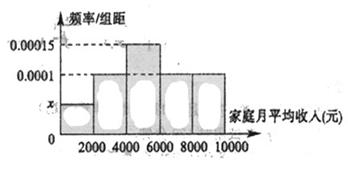
某企业准备给该校高三学生发放助学金,发放规定为:家庭收入在4000元以下(≤4000元)的每位同学得助学金2000元,家庭收入在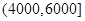 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在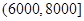 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在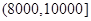 (元)间的同学不发助学金.
(元)间的同学不发助学金.
(1)求频率分布直方图中的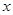 值;
值;
(2)求该校高三年级学生中获得1500元助学金以上(≥1500元)的人数.