(本小题满分12分)
在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q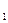
为0.25，在B处的命中率为q
，该同学选择先在A处投一球，以后都在B处投，用
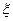表示该同学投篮训练结束后所得的总分，其分布列为
| |
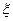0 |
2 |
3 |
4 |
5 |
| p |
0.03 |
P1 |
P2 |
P3 |
P4 |
（1） 求q的值；
（2） 求随机变量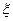的数学期望E;
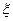（3） 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
如图，正方体ABCD—A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．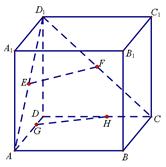
（1）求GH长的取值范围；
（2）当GH取得最小值时，求证：EH与FG共面；并求出此时EH与FG的交点P到直线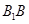
的距离.
如图，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点，且AB=AD，BC=DC．
（1）求证：
平面EFGH；
（2）求证：四边形EFGH是矩形．
如图，正方体ABCD—A1B1C1D1中，E为AB中点，F为正方形BCC1B1的中心.
（1）求直线EF与平面ABCD所成角的正切值；
（2）求异面直线A1C与EF所成角的余弦值．
已知定义在R上的函数f(x)=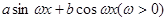
的周期为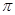
，且对一切x
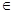R，都有f(x)
；
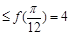（1）求函数f(x)的表达式；
（2）若g(x)=f(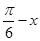
),求函数g(x)的单调增区间；
已知函数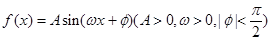
在一个周期内的图像下图所示。
（1）求函数的解析式；
（2）设
，且方程
有两个不同的实数根，求实数m的取值范围和这两个根的和。