(本小题满分8分)
如图,在 中,D、E分别是AB、AC的中点,DM=
中,D、E分别是AB、AC的中点,DM= DE,若
DE,若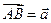 ,
,
(1)用 表示
表示 ;
;
(2)若N为线段BC上的点,且BN= BC,用向量方法证明:A、M、N三点共线.
BC,用向量方法证明:A、M、N三点共线. 
已知函数
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求 的值.
的值.
记函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 ,集合
,集合 .
.
(Ⅰ)求集合 ,
,
 ;
;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
计算:
(Ⅰ)
(Ⅱ)
设直线l1:y=k1x+1,l2:y=k2x-1,其中实数k1,k2满足k1k2+1=0.
(Ⅰ)证明:直线l1与l2相交;(Ⅱ)试用解析几何的方法证明:直线l1与l2的交点到原点距离为定值.(Ⅲ)设原点到l1与l2的距离分别为d1和d2求d1+d2的最大值
如图:AD=2,AB=4的长方形 所在平面与正
所在平面与正 所在平面互相垂直,
所在平面互相垂直, 分别为
分别为 的中点.
的中点.
(1)求四棱锥 -
- 的体积;
的体积;
(2)求证: 平面
平面 ;
;
(3)试问:在线段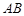 上是否存在一点
上是否存在一点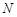 ,使得平面
,使得平面 平面
平面 ?若存在,试指出点
?若存在,试指出点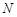 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.