已知点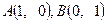 ,
,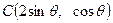 .
.
(Ⅰ)若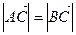 , 求
, 求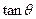 的值;
的值;
(Ⅱ)设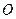 为坐标原点, 点C在第一象限, 求函数
为坐标原点, 点C在第一象限, 求函数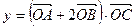 的单调递增区间与值域.
的单调递增区间与值域.
已知函数 ,其中
,其中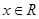 ,
,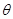 为参数,且
为参数,且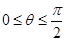 .
.
(1)当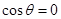 时,判断函数
时,判断函数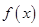 是否有极值;
是否有极值;
(2)要使函数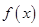 的极小值大于零,求参数
的极小值大于零,求参数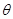 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数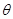 ,函数
,函数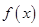 在区间
在区间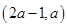 内都是增函数,求实数
内都是增函数,求实数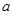 的取值范围.
的取值范围.
已知数列 的前
的前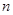 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)已知数列 的通项公式
的通项公式 ,记
,记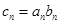 ,求数列
,求数列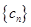 的前
的前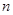 项和
项和 .
.
已知函数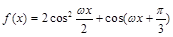 (其中
(其中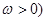 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求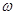 的值,并求函数
的值,并求函数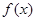 的单调递减区间;
的单调递减区间;
(Ⅱ)在锐角 中,
中,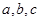 分别是角
分别是角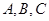 的对边,若
的对边,若
 的面积为
的面积为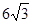 ,求
,求 的外接圆面积.
的外接圆面积.
已知数列 为等差数列,且
为等差数列,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足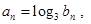 求数列
求数列 的前
的前 项和
项和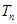 .
.
设函数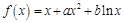 ,曲线
,曲线 过点
过点 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2.
(1)求a和b的值; (2)证明: .
.