在平面直角坐标系 中,点
中,点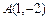 ,
,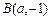 ,
,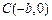 ,且
,且 .
.
(1)若点 、
、 、
、 在直线
在直线 上,求
上,求
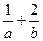 的最小值,并求此时直线
的最小值,并求此时直线 的方程;
的方程;
(2)若以线段 、
、 为邻边的平行四边形两条对角线的长相等,且
为邻边的平行四边形两条对角线的长相等,且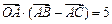 ,求
,求 、
、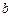 的值.
的值.
(本小题满分12分)
如图:在三棱锥D-ABC中,已知 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且

(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.
(本小题满分12分)
已知  且
且 ;
; :集合
:集合 ,且
,且 .若
.若 ∨
∨ 为真命题,
为真命题, ∧
∧ 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,
,
设向量 ,
, ,
, 
(Ⅰ)若 ∥
∥ ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥ ,边长
,边长 ,
, ,求
,求 的面积.
的面积.
(本小题满分12分)已知函数
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(本题12分)已知椭圆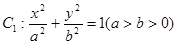 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线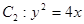 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
(I)求椭圆C1的方程;(II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线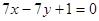 上,求直线AC的方程。
上,求直线AC的方程。