(本小题满分14分)已知函数f(x)=alnx+x2(a为实常数).
(Ⅰ)若a=-2,求证:函数f(x)在(1,+∞)上是增函数;
(Ⅱ)求函数f(x)在[1,e]上的最小值及相应的x值;
选修4—4:不等式选讲
已知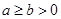 ,求证:
,求证: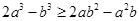 .
.
(本小题满分10分)选修4—3:坐标系与参数方程
已知直线l经过点P( ,1),倾斜角α=
,1),倾斜角α=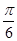 ,圆C的极坐标方程为
,圆C的极坐标方程为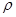 =
=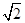 cos(θ-
cos(θ-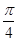 ).
).
(Ⅰ)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(Ⅱ)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积.
(本小题满分10分,选修4—2:矩阵与变换)
已知矩阵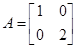 ,
,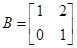 ,若矩阵
,若矩阵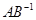 对应的变换把直线
对应的变换把直线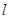 变为直线
变为直线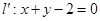 ,求直线
,求直线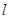 的方程.
的方程.
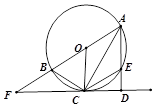
(本小题满分10分)选修4—1:几何证明选讲
如图,已知 是
是 的直径,
的直径,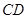 是
是 的切线,
的切线, 为切点,
为切点,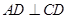 ,交
,交 于点
于点 ,连接
,连接 、
、 、
、 、
、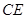 ,延长
,延长 交
交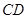 于
于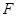 .
.
(1)证明: ;
;
(2)证明: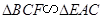 .
.
(本小题满分14分)设函数 (
( ).
).
(1)当 时,求
时,求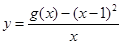 的极值;
的极值;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点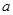 ,
, ,且
,且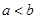 ,记
,记 表示不大于
表示不大于 的最大整数,试比较
的最大整数,试比较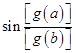 与
与 的大小.
的大小.