(本小题满分8分)
一个学校的足球队、篮球队和排球队分别有28,22,17名成员,一些成员不止参加一支球队,具体情况如图所示,随机选取的一名成员:
(1) 属于不止1支球队的概率是多少?
(2) 属于不超过2支球队的概率是多少?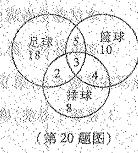
已知 ,且
,且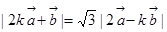 (
(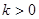 ),设
),设 与
与 的夹角为
的夹角为
(1)求 与
与 的函数关系式;
的函数关系式;
(2)当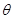 取最大值时,求
取最大值时,求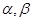 满足的关系式.
满足的关系式.
如图,在某点B处测得建筑物AE的顶端A的仰角为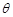 ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2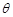 ,再继续前进10
,再继续前进10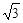 m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4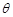 ,求建筑物AE的高度。
,求建筑物AE的高度。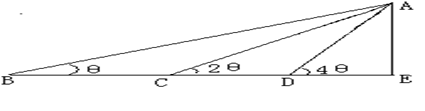
在△ABC中,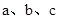 是角
是角 所对的边,且
所对的边,且 .
.
(1)求角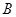 的大小;(2)若
的大小;(2)若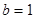 ,求△ABC周长的最大值。
,求△ABC周长的最大值。
定义:已知函数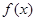 与
与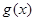 ,若存在一条直线
,若存在一条直线 ,使得对公共定义域内的任意实数均满足
,使得对公共定义域内的任意实数均满足 恒成立,其中等号在公共点处成立,则称直线
恒成立,其中等号在公共点处成立,则称直线 为曲线
为曲线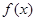 与
与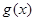 的“左同旁切线”.已知
的“左同旁切线”.已知 .
.
(1)试探求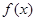 与
与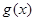 是否存在“左同旁切线”,若存在,请求出左同旁切线方程;若不存在,请说明理由.
是否存在“左同旁切线”,若存在,请求出左同旁切线方程;若不存在,请说明理由.
(2)设 是函数
是函数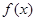 图象上任意两点,
图象上任意两点,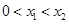 ,且存在实数
,且存在实数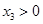 ,使得
,使得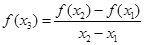 ,证明:
,证明: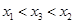 .
.
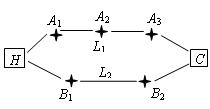
李先生家住 小区,他工作在
小区,他工作在 科技园区,从家开车到公司上班路上有
科技园区,从家开车到公司上班路上有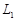 、
、 两条路线(如图),
两条路线(如图),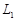 路线上有
路线上有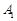 、
、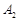 、
、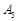 三个路口,各路口遇到红灯的概率均为
三个路口,各路口遇到红灯的概率均为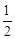 ;
; 路线上有
路线上有 、
、 两个路口,各路口遇到红灯的概率依次为
两个路口,各路口遇到红灯的概率依次为 ,
, .
.
(Ⅰ)若走 路线,求最多遇到1次红灯的概率;
路线,求最多遇到1次红灯的概率;
(Ⅱ)若走 路线,求遇到红灯次数
路线,求遇到红灯次数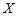 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.