(本小题满分13分)
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为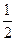 ,且经过点
,且经过点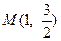 ,过点
,过点 的直线
的直线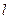 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点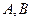 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存直线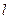 ,满足
,满足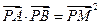 ?若存在,求出直线
?若存在,求出直线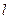 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分14分)已知半径为 的圆的圆心在
的圆的圆心在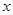 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线
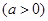 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线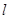 过点
过点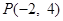 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(本小题满分14分)函数 。
。
(1)求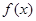 的周期;(2)
的周期;(2)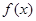 在
在 上的减区间;
上的减区间;
(3)若
 ,
, ,求
,求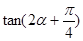 的值。
的值。
(本小题满分12分)如图,函数y=2sin(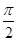 x+φ) x∈R , 其中0≤φ≤
x+φ) x∈R , 其中0≤φ≤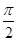 的图象与y轴交于点(0,1).
的图象与y轴交于点(0,1).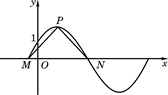
(Ⅰ)求φ的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求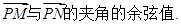
(本小题满分12分)已知函数 ,
,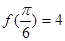 ,
,
(1)求实数a的值;
(2)求函数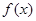 在
在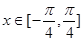 的值域。
的值域。