(本小题满分12分)
某旅游公司为 3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团从中任选一条。
3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团从中任选一条。
(I)求3个旅游团选择3条不同的旅游线路的概率;
(II)求恰有2条旅游线路没有被选择的概率;
(III)求选择甲旅游线路的旅游团数的分布列及数学期望。
如图,四棱锥 中,底面
中,底面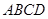 为菱形,
为菱形,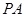 ⊥平面
⊥平面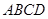 ,
, 交
交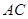 于点
于点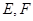 是线段
是线段 中点,
中点, 为线段
为线段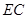 中点.
中点.
(1)求证: //平面
//平面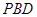 ;
;
(2)求证: ⊥
⊥ .
.
(本小题满分14分)经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间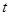 (天)的函数,且销售量近似满足
(天)的函数,且销售量近似满足 (件),价格近似满足
(件),价格近似满足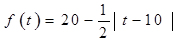 (元).
(元).
(1)试写出该种商品的日销售额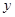 与时间
与时间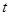 (
( )的函数关系表达式;
)的函数关系表达式;
(2)求该种商品的日销售额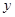 的最大值与最小值
的最大值与最小值
已知向量 ,其中
,其中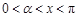 .
.
(1)若 ,求函数
,求函数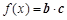 的最小值及相应x的值;
的最小值及相应x的值;
(2)若 与
与 的夹角为
的夹角为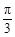 ,且
,且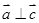 ,求
,求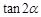 的值.
的值.
(本小题满分10分)已知函数 .
.
(1)求函数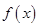 的定义域并判断函数的奇偶性;
的定义域并判断函数的奇偶性;
(2)设 ,若记
,若记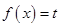 ,求函数
,求函数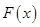 的最大值的表达式
的最大值的表达式 .
.
已知圆 .
.
(1)此方程表示圆,求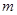 的取值范围;
的取值范围;
(2)若(1)中的圆与直线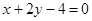 相交于
相交于 、
、 两点,且
两点,且 (
( 为坐标原点),求
为坐标原点),求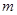 的值;
的值;
(3)在(2)的条件下,求以 为直径的圆的方程.
为直径的圆的方程.