已知向量 ,其中
,其中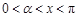 .
.
(1)若 ,求函数
,求函数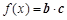 的最小值及相应x的值;
的最小值及相应x的值;
(2)若 与
与 的夹角为
的夹角为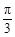 ,且
,且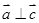 ,求
,求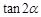 的值.
的值.
4-1:几何证明选讲(本小题满分10分)
如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.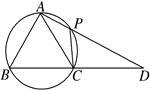
(1)求证: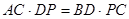
(2)若△ABC是面积为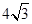 的等边三角形,求AP·AD的值
的等边三角形,求AP·AD的值
(本小题满分12分)已知函数
(1)讨论函数 的单调性
的单调性
(2)若函数 与函数
与函数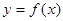 的图像关于原点对称且
的图像关于原点对称且 就函数
就函数 分别求解下面两问:
分别求解下面两问:
(Ⅰ)问是否存在过点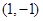 的直线与函数
的直线与函数 的图象相切? 若存在,有多少条?若不存在,说明理由
的图象相切? 若存在,有多少条?若不存在,说明理由
(Ⅱ)求证:对于任意正整数 ,均有
,均有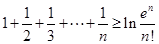 (
(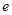 为自然对数的底数)
为自然对数的底数)
(本小题满分12分)在平面直角坐标系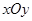 中,已知抛物线
中,已知抛物线 :
: ,过点
,过点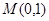 的直线
的直线 与抛物线
与抛物线 分别相交于
分别相交于 两个不同的点.
两个不同的点.
(1)以AB为直径的圆是否过定点,若是请求出该点坐标。若不是,请说明理由
(2)过 两点分别作抛物线
两点分别作抛物线 的切线
的切线 ,设它们相交于点
,设它们相交于点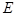 ,求
,求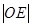 的取值范围
的取值范围
(本小题满分12分)如图,正方形 所在的平面垂直,且
所在的平面垂直,且 等于
等于 。设
。设 、
、 分别为
分别为 、
、 上的动点,(不包括端点)
上的动点,(不包括端点)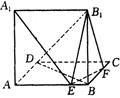
(1)若 .求证:
.求证:
(2)设 ,求异面直线
,求异面直线 与
与 所成的角取值范围
所成的角取值范围
(本小题满分12分) 学生的学习能力参数 可有效衡量学生的综合能力,
可有效衡量学生的综合能力, 越大,综合能力越强,为推动数学知识的发展,提高学生的综合能力。某校根据学生的学习能力参数
越大,综合能力越强,为推动数学知识的发展,提高学生的综合能力。某校根据学生的学习能力参数 将参加数学竞赛小组的学生分成了如下三类:
将参加数学竞赛小组的学生分成了如下三类:
学习能力参数 |
学习能力参数 |
||
 |
 |
 |
|
| 学生人数(人) |
15 |
10 |
 |
某研究性学习小组,从该竞赛小组中按分层抽样的方法随机选取了 人,根据其学习能力参数
人,根据其学习能力参数 ,作出了频率与频数的统计表:
,作出了频率与频数的统计表:
| 分组 |
频数(人) |
频率 |
 |
3 |
|
 |
 |
 |
 |
 |
|
| 合计 |
 |
 |
(1)求 ,
, ,
, ,
, 的值
的值
(2)规定:学习能力参数 不少于70称为优秀。若从这
不少于70称为优秀。若从这 人中任选
人中任选 人,记抽到到的优秀人数为随机变量
人,记抽到到的优秀人数为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望