在平面直角坐标系xOy中，已知圆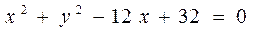
的圆心为Q,过点
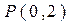且斜率为
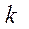的直线与圆Q相交于不同的两点A、B.
（1）求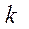的取值范围；
（2）是否存在常数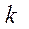，使得向量
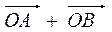与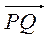
共线？如果存在，求出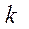的值；如果不存在，请说明理由。
（本小题满分14分）
动圆G与圆
外切，同时与圆
内切，设动圆圆心G的轨迹为
。
（1）求曲线的方程；
（2）直线
与曲线相交于不同的两点
，以
为直径作圆
，若圆C与
轴相交于两点
，求
面积的最大值；
（3）已知
，直线
与曲线相交于
两点（均不与
重合），且以
为直径的圆过点
，求证：直线
过定点，并求出该点坐标。
如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱
,
,底面
为直角梯形，其中BC∥AD, AB⊥AD, 
,O为AD中点.
(1)求直线
与平面
所成角的余弦值;
(2)求
点到平面
的距离
(3)线段
上是否存在点
,使得二面角
的余弦值为
?若存在,求出
的值;若不存在,请说明理由.
（本小题满分12分）
设函数
.
（Ⅰ）解不等式
；
（Ⅱ）对于实数
，若
，求证
．
题满分12分）
.如图，平行六面体ABCD－A1B1C1D1中，∠BAD＝∠BAA1＝∠DAA1＝60°，
（1）当AA1＝3，AB＝2，AD＝2，求AC1的长；
（2）当底面ABCD是菱形时，求证：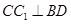
（本小题满分12分）
设命题
：方程
表示焦点在坐标轴上的双曲线，命题
：
。
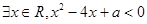（1）写出命题的否定；
（2）若“或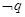
”为真命题，求实数
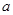的取值范围。