如图1，在三棱锥P－ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上一点，它的正(主)视图和侧(左)视图如图2所示．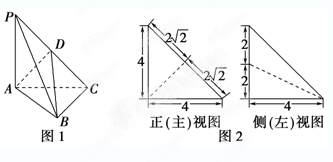
(1)证明：AD⊥平面PBC；
(2)求三棱锥D－ABC的体积；
(3)在∠ACB的平分线上确定一点Q，使得PQ∥平面ABD，并求此时PQ的长．
（本小题满分14分）在平面直角坐标系xOy中，椭圆C：
（a＞b＞0）的上顶点到焦点的距离为2，离心率为
．
（1）求a，b的值．
（2）设P是椭圆C长轴上的一个动点，过点P作斜率为k的直线l交椭圆C于A、B两点．
（ⅰ）若k＝1，求△OAB面积的最大值；
（ⅱ）若PA2＋PB2的值与点P的位置无关，求k的值．
（本小题满分14分）已知函数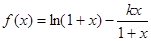
，
．
（1）讨论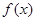
的单调区间；
（2）当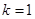
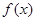时，求在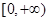
上的最小值，并证明
．
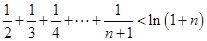（本小题满分14分）已知四棱锥
中，
，底面
是边长为
的菱形，
，
．
（Ⅰ）求证：
；
（Ⅱ）设
与
交于点
，
为
中点，若二面角
的正切值为
，求
的值．
（本小题满分14分）已知单调递增的等比数列
满足：
，且
是
的等差中项．
（1）求数列的通项公式；
（2）若
，
，求使
成立的正整数
的最小值．
（本小题满分12分）某中学号召本校学生在本学期参加市创办卫生城的相关活动，学校团委对该校学生是否关心创卫活动用简单抽样方法调查了
位学生（关心与不关心的各一半），
结果用二维等高条形图表示，如图．
（1）完成列联表，并判断能否有
℅的把握认为是否关心创卫活动与性别有关？
 |
0．10 |
0．05 |
0．01 |
 |
2．706 |
3．841 |
6．635 |
（参考数据与公式：
；
| 女 |
男 |
合计 |
|
| 关心 |
500 |
||
| 不关心 |
500 |
||
| 合计 |
524 |
1000 |
（2）已知校团委有青年志愿者100名，他们已参加活动的情况记录如下：
| 参加活动次数 |
1 |
2 |
3 |
| 人数 |
10 |
50 |
40 |
（i）从志愿者中任选两名学生，求他们参加活动次数恰好相等的概率；
（ii）从志愿者中任选两名学生，用
表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望
．