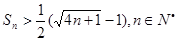(本小题满分13分) 已知⊙O经过三点(1,3)、(-3,-1)、(-1,3),⊙M是以两点(7,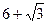 ),(9,
),(9,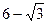 )为直径的圆.过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
)为直径的圆.过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(1)求⊙O及⊙M的方程;
(2)若直线PA与⊙M的另一交点为Q,当弦PQ最长时,求直线PA的方程;
(3)求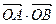 的最大值与最小值.
的最大值与最小值.
(本小题满分12分)设集合A={x|x2<4},B={x|1<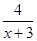 }.
}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
(本小题满分10分)(1)将形如 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 =a11a22-a12a21,试计算二阶行列式
=a11a22-a12a21,试计算二阶行列式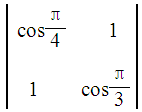 的值;
的值;
(2)已知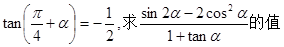 。
。
已知平面上的动点P(x,y)及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是k1,k2,且k1·k2=-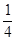 .
.
(1)求动点P的轨迹C的方程;
(2)已知直线l:y=kx+m与曲线C交于M,N两点,且直线BM、BN的斜率都存在,并满足kBM·kBN=-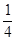 ,求证:直线l过原点.
,求证:直线l过原点.
如图,在四棱锥 中,底面
中,底面 四边长为1的菱形,
四边长为1的菱形, ,
,  ,
,  ,
, 为
为 的中点,
的中点, 为
为 的中点
的中点
(Ⅰ)证明:直线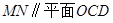
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
已知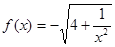 ,数列
,数列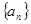 的前
的前 项和为
项和为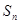 ,点
,点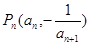 在曲线
在曲线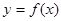 上
上 ,
,
且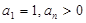
(1)求数列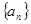 的通项公式(2) 求证:
的通项公式(2) 求证: