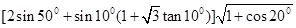如图,在四棱锥
中,
底面
,
是
的中点.
(Ⅰ)证明
;
(Ⅱ)证明
平面
;
(Ⅲ)求二面角
的大小.
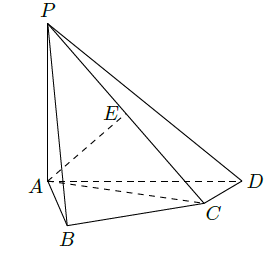
(本小题满分12分)设命题
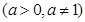 是减函数,命题
是减函数,命题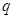 :关于
:关于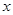
的不等式 的解集为
的解集为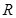 ,如果“
,如果“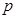 或
或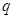 ”为真命题,“
”为真命题,“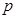 且
且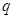 ”为假命题,求
”为假命题,求
实数 的取值范围.
的取值范围.
(本小题满分10分)国家有甲,乙两个射击队,若两个队共进行了8次热身赛,
各队的总成绩见下表:
| 甲队 |
403 |
390 |
397 |
404 |
388 |
400 |
412 |
406 |
| 乙队 |
417 |
401 |
410 |
416 |
406 |
421 |
398 |
411 |
分别求两个队总成绩的样本平均数和样本方差,根据计算结果,若选一个代表队参加奥运会比赛,你认为应该选哪一个队?
定义在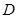 上的函数
上的函数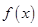 ,如果满足:对任意
,如果满足:对任意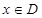 ,存在常数
,存在常数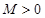 ,都有
,都有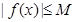 成立,则称
成立,则称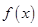 是
是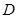 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数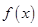 的上界.
的上界.
(1)判断函数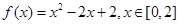 是否是有界函数,请写出详细判断过程;
是否是有界函数,请写出详细判断过程;
(2)试证明:设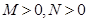 ,若
,若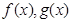 在
在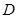 上分别以
上分别以 为上界,
为上界,
求证:函数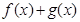 在
在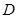 上以
上以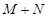 为上界;
为上界;
(3)若函数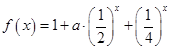 在
在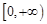 上是以3为上界的有界函数,
上是以3为上界的有界函数,
求实数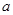 的取值范围.
的取值范围.
已知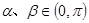 ,且
,且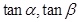 是方程
是方程 的两根.
的两根.
(1)求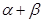 的值.(2)求
的值.(2)求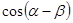 的值.
的值.
化简