在数列
中,
,其中
.
(Ⅰ)求数列
的通项公式;
(Ⅱ)求数列
的前
项和
;
(Ⅲ)证明存在
,使得
对任意
均成立.
已知函数f(x)=x2+ +alnx(x>0).
+alnx(x>0).
(1)若f(x)在[1,+∞)上单调递增,求a的取值范围.
(2)若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1,x2总有不等式 [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
已知函数f(x)=ex+ax,g(x)=ax-lnx,其中a≤0.
(1)求f(x)的极值.
(2)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.
已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x- +
+ .
.
(1)求函数f(x)的最小值.
(2)对于∀x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
已知函数f(x)=2x,g(x)=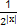 +2.
+2.
(1)求函数g(x)的值域.
(2)求满足方程f(x)-g(x)=0的x的值.
设函数f(x)=log3(9x)·log3(3x), ≤x≤9.
≤x≤9.
(1)若m=log3x,求m的取值范围.
(2)求f(x)的最值,并给出最值时对应的x的值.