下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
（吨）与相应的生产能耗
（吨标准煤）的几组对照数据
(1) 请画出上表数据的散点图；
(2)请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
；
(3)已知该厂技术改造前
吨甲产品能耗为
吨标准煤.试根据（２）求出的线性回归方程，预测生产
吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考数据:
）
如图所示茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩．乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以a表示．
(1)若甲、乙两个小组的数学平均成绩相同，求a的值；
(2)求乙组平均成绩超过甲组平均成绩的概率；
(3)当a＝2时，分别从甲、乙两组同学中各随机选取一名同学，求这两名同学的数学成绩之差的绝对值不超过2分的概率．
已知函数f(x)＝4sinxcos(x－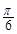
)－1
(1)求函数f(x)的最小正周期； (2)当x∈[－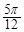
π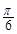，]时，求函数f(x)的取值范围．
已知命题p:方程
有两个不等的负根;命题q：方程
无实根．若
为真，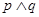
为假，试求实数m的取值范围．
设函数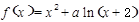
、
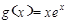，且f（x）存在两个极值点
、
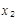，其中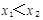
.
（Ⅰ）求实数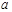
的取值范围；
（Ⅱ）求
的最小值；
（Ⅲ）证明不等式：
.
已知函数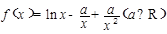
.
（Ⅰ）若a＝1，求函数f（x）的极值；
（Ⅱ）若f（x）在[1，＋∞）内为单调增函数，求实数
的取值范围；
（Ⅲ）对于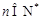
，求证：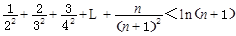
.