已知函数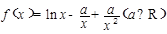 .
.
(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)若f(x)在[1,+∞)内为单调增函数,求实数 的取值范围;
的取值范围;
(Ⅲ)对于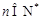 ,求证:
,求证: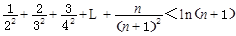 .
.
等比数列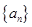 中的前三项a1、a2、a3分别是下面数阵中第一、二、三行中的某三个数,且三个数不在同一列.
中的前三项a1、a2、a3分别是下面数阵中第一、二、三行中的某三个数,且三个数不在同一列.
(1)求此数列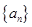 的通项公式;
的通项公式;
(2)若数列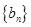 满足
满足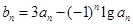 ,求数列
,求数列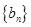 的前n项和
的前n项和 .
.
如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,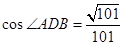 .
.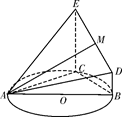
(1)求证:平面AEC⊥平面BCED;
(2)试问线段DE上是否存在点M,使得直线AM与平面ACE所成角的正弦值为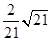 ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
某电视台拟举行由选手报名参加的比赛类型的娱乐节目,选手进入正赛前需通过海选,参加海选的选手可以参加A、B、C三个测试项目,只需通过一项测试即可停止测试,通过海选.若通过海选的人数超过预定正赛参赛人数,则优先考虑参加海选测试次数少的选手进入正赛.甲选手通过项目A、B、C测试的概率为分别为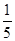 、
、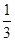 、
、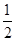 , 且通过各次测试的事件相互独立.
, 且通过各次测试的事件相互独立.
(1)若甲选手先测试A项目,再测试B项目,后测试C项目,求他通过海选的概率;若改变测试顺序,对他通过海选的概率是否有影响?说明理由;
(2)若甲选手按某种顺序参加海选测试,第一项能通过的概率为p1,第二项能通过的概率为p2,第三项能通过的概率为p3,设他通过海选时参加测试的次数为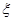 ,求
,求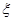 的分布列和期望(用p1、p2、p3表示);并说明甲选手按怎样的测试顺序更有利于他进入正赛.
的分布列和期望(用p1、p2、p3表示);并说明甲选手按怎样的测试顺序更有利于他进入正赛.
设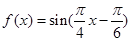
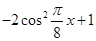 .
.
(1)求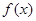 的最小正周期;
的最小正周期;
(2)若函数y=f(x)与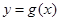 的图象关于直线x=1对称,求当
的图象关于直线x=1对称,求当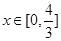 时y=g(x)的最大值.
时y=g(x)的最大值.
(本小题满分14分)已知函数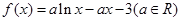 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数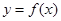 的图像在点
的图像在点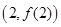 处的切线的倾斜角为
处的切线的倾斜角为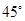 ,对于任意的
,对于任意的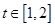 ,函数
,函数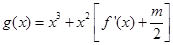 在区间
在区间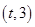 上总不是单调函数,求
上总不是单调函数,求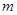 的取值范围;
的取值范围;
(3)求证: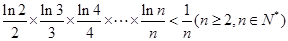 .
.