某项选拔共有三轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考试，否则即被淘汰，已知某选手能正确回答第一、二、三轮的问题的概率分别为
、
、
，且各轮问题能否正确回答互不影响.
（Ⅰ）求该选手被淘汰的概率；
（Ⅱ）该选手在选拔中回答问题的个数记为
，求随机变量
的分布列与数数期望.（注：本小题结果可用分数表示）
沿一条小路前进，从A到B，方位角（从正北方向顺时针转到AB方向所成的角）是
50°，距离是3 km，从B到C，方位角是110°，距离是3 km，从C到D,方位角是140°，距离是（9+3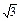
）km.试画出示意图，并计算出从A到D的方位角和距离（结果保留根号）.
要测量对岸A、B两点之间的距离，选取相距
km的C、D两点，并测得∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°，求A、B之间的距离.
在△ABC中，角A、B、C的对边分别为a、b、c，已知a+b=5，c=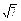
，且4sin2
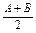-cos2C=
.
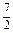(1)求角C的大小；
（2）求△ABC的面积.
已知a、b、c是△ABC的三边长，关于x的方程ax2-2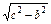
x-b="0" (a＞c＞b)的两根之差的平方等于4，△ABC的面积S=10
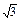，c=7.
（1）求角C；
（2）求a，b的值.
在△ABC中，cosB=-
，cosC=
.
（1）求sinA的值；
（2）△ABC的面积S△ABC=
，求BC的长.