如图,在底面为直角梯形的四棱锥
中,
,
,
,
,
,
,
.

(Ⅰ)求证: ;
(Ⅱ)求二面角 的大小.
(本小题满分12分)
已知中心在原点,焦点在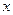 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为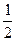 ,且经过点
,且经过点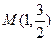 ,过点P(2,1)的直线
,过点P(2,1)的直线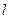 与椭圆C相交于不同的两点A、B.
与椭圆C相交于不同的两点A、B.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存直线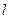 ,满足
,满足 ?
? 若存在,求出直线
若存在,求出直线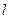 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)
设 函数
函数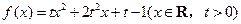 .
.
(Ⅰ)求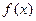 的最小值
的最小值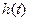 ;
;
(Ⅱ)若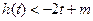 对
对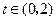 恒成立,求实数
恒成立,求实数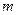 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆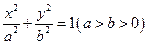 短轴
短轴 的一个端点
的一个端点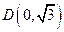 ,离心率
,离心率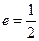 .过
.过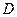 作直线
作直线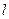 与椭圆交于另一点
与椭圆交于另一点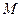 ,与
,与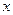 轴交于点
轴交于点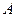 (
( 不同于原点
不同于原点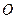 ),点
),点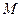 关于
关于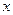 轴的对称点为
轴的对称点为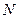 ,直线
,直线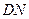 交
交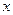 轴于点
轴于点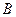 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求 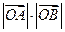 的值.
的值.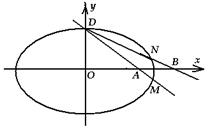
本小题满分12分)已知函数f(x)=ax3+mx2-m2x+1(m<0)在点x=-m处取得极值.
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间.
本小题满分10分)求圆心在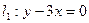 上,与
上,与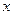 轴相切,且被直线
轴相切,且被直线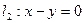 截得弦长为
截得弦长为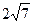 的圆的方程
的圆的方程 .
.