已知各项全不为零的数列
的前k项和为
,且
,其中
.
(Ⅰ)求数列
的通项公式;
(Ⅱ)对任意给定的正整数
,数列
满足
.求
.
(本小题满分14分)数列 的各项均为正数,
的各项均为正数,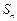 为其前
为其前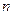 项和,对于任意
项和,对于任意 ,总有
,总有 成等差数列.
成等差数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列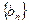 的前
的前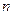 项和为
项和为 ,且
,且 ,求证:对任意实数
,求证:对任意实数 (
(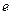 是常数,
是常数,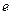 =2.71828
=2.71828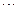 )和任意正整数
)和任意正整数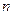 ,总有
,总有
 2;
2;
(Ⅲ) 已知正数数列 中,
中, .,求数列
.,求数列 中的最大项.
中的最大项.
郑已知定点A(0,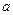 )(
)(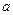 >0),直线
>0),直线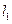 :
: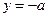 交
交 轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
(I)求动点C的轨迹E的方程;
(Ⅱ)设倾斜角为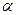 的直线
的直线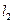 过点A,交轨迹E于两点 P、Q,交直线
过点A,交轨迹E于两点 P、Q,交直线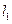 于点R.
于点R.
(1)若tan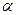 =1,且ΔPQB的面积为
=1,且ΔPQB的面积为 ,求
,求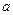 的值;
的值;
(2)若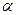 ∈[
∈[ ,
, ],求|PR|·|QR|的最小值.
],求|PR|·|QR|的最小值.
如图,正方形ABCD和四边形ACEF所在的平面互相垂直。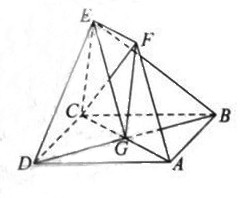
EF//AC,AB=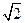 ,CE=EF=1
,CE=EF=1
(Ⅰ)求证:AF//平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(本小题满分12分)某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.

表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率
分别是多少;
(3)由以上统计数据完成下面 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| 甲流水线 |
乙流水线 |
合计 |
|
| 合格品 |
 |
 |
|
| 不合格品 |
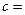 |
 |
|
| 合 计 |
 |
附:下面的临界值表供参考:
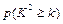 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
(本小题满分12分) 已知向量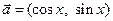 ,
, ,
, .
.
(1)若 求向量
求向量 与
与 的夹角;
的夹角;
(2)当 时,求函数
时,求函数 的最大值。
的最大值。