已知半椭圆
与半椭圆
组成的曲线称为"果圆",其中
.如图,设点
是相应椭圆的焦点,
,
和
,
是"果圆" 与
,
轴的交点,
(1)若三角形
是边长为1的等边三角形,求"果圆"的方程;
(2)若
,求
的取值范围;
(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦。是否存在实数
,使得斜率为
的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有
的值;若不存在,说明理由.

已知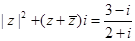 ,其中
,其中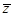 是
是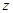 的共轭复数,求复数
的共轭复数,求复数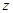 .
.
已知函数 .
.
(1)若曲线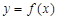 在
在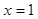 处的切线的方程为
处的切线的方程为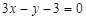 ,求实数a的值;
,求实数a的值;
(2)求证: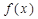 ≥0恒成立的充要条件是
≥0恒成立的充要条件是 ;
;
(3)若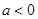 ,且对任意
,且对任意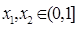 ,都有
,都有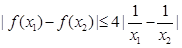 ,求实数a的取值范围.
,求实数a的取值范围.
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: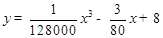 (
(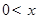 ≤120).已知甲、乙两地相距100千米.
≤120).已知甲、乙两地相距100千米.
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
如图,四棱锥 中,底面
中,底面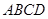 为平行四边形,
为平行四边形, ,
,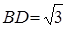 ,
,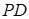 ⊥底面
⊥底面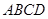 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为 ,求
,求 与平面
与平面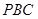 所成角的正弦值.
所成角的正弦值.
设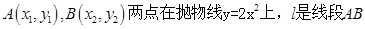 的垂直平分线.
的垂直平分线.
(1)当且仅当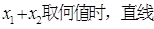
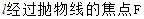 ?
?
(2)当直线的斜率为2时,求 轴上截距的取值范围.
轴上截距的取值范围.