已知数列
中的相邻两项
,是关于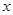 的方程
的两个根,且
.
的方程
的两个根,且
.
(I)求
,
,
,
;
(II)求数列
的前
项和
;
(Ⅲ)记
,
,
求证: .
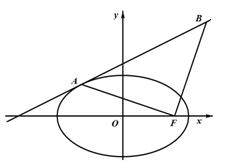
如图所示,椭圆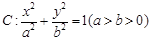 与直线
与直线 相切于点
相切于点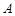 .
.
(1)求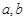 满足的关系式,并用
满足的关系式,并用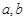 表示点
表示点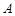 的坐标;
的坐标;
(2)设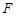 是椭圆的右焦点,若
是椭圆的右焦点,若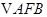 是以
是以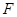 为直角顶点的等腰直角三角形,求椭圆
为直角顶点的等腰直角三角形,求椭圆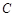 的标准方程
的标准方程
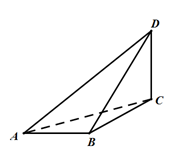
如图所示,在三棱锥 中,
中,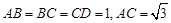 ,平面
,平面 ⊥平面
⊥平面 ,
, .
.
(1)求证: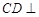 平面
平面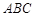 ;
;
(2)求直线 与平面
与平面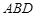 所成角的正弦值.
所成角的正弦值.
已知函数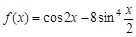 .
.
(1)求函数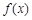 的最小正周期;
的最小正周期;
(2)求函数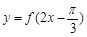 在
在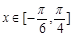 上的值域
上的值域
(本小题满分14分)已知函数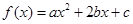
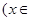
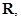
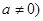
(Ⅰ)若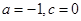 ,且
,且 在
在 上的最大值为
上的最大值为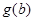 ,求
,求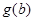 ;
;
(Ⅱ)若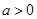 ,函数
,函数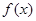 在
在 上不单调,且它的图象与
上不单调,且它的图象与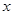 轴相切,求
轴相切,求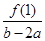 的最小值.
的最小值.
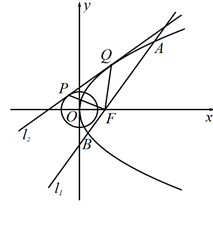
(本小题满分15分)如图,设抛物线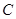 :
: 的焦点为
的焦点为 ,过点
,过点 的直线
的直线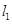 交抛物线
交抛物线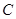 于
于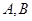 两点,且
两点,且 ,线段
,线段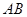 的中点到
的中点到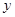 轴的距离为
轴的距离为 .
.
(Ⅰ)求抛物线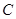 的方程;
的方程;
(Ⅱ)若直线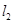 与圆
与圆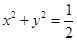 切于点
切于点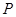 ,与抛物线
,与抛物线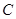 切于点
切于点 ,求
,求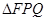 的面积.
的面积.