(本小题满分14分)已知函数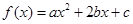
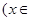
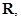
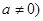
(Ⅰ)若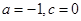 ,且
,且 在
在 上的最大值为
上的最大值为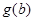 ,求
,求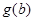 ;
;
(Ⅱ)若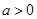 ,函数
,函数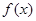 在
在 上不单调,且它的图象与
上不单调,且它的图象与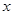 轴相切,求
轴相切,求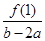 的最小值.
的最小值.
设函数 的图像在
的图像在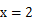 处的切线与直线
处的切线与直线 平行。
平行。
(1)求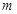 的直线;
的直线;
(2)求函数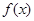 在区间
在区间 上的最小值;
上的最小值;
(3)若 ,利用结论(2)证明:
,利用结论(2)证明: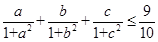
已知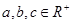 ,求证:
,求证: 。
。
求直线 被曲线
被曲线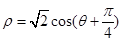 所截的弦长。
所截的弦长。
调查1000名50岁以上有吸烟习惯与患慢性气管炎的人的情况,获数据如下表:
| 患慢性气管炎 |
未患慢性气管炎 |
总计 |
|
| 吸烟 |
360 |
320 |
680 |
| 不吸烟 |
140 |
180 |
320 |
| 合计 |
500 |
500 |
1000 |
试问:根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为吸烟习惯与患慢性气管炎病有关?参考数据如下:
(k=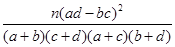 ,且P(K2≥6.635)≈0.01,)
,且P(K2≥6.635)≈0.01,)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请在给出的坐标系内画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的回归直线方程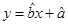 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为92吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数据:3×2.5+4×3+5×4+6×4.5=66.5)
(参考公式: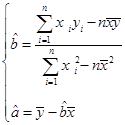 )
)