已知函数f(x)ax4lnxbx4c(x＞0)在x1处取得极-优题课

已知函数 $f (x) = a x^{4} \ln x + b x^{4} - c (x ＞ 0)$ 在 $x = 1$ 处取得极值 $- 3 - c$ ，其中 $a, b, c$ 为常数。
（1）试确定 $a, b$ 的值；
（2）讨论函数 $f (x)$ 的单调区间；
（3）若对任意 $x > 0$ ，不等式 $f (x) \geq - 2 c^{2}$ 恒成立，求 $c$ 的取值范围.

科目数学题型解答题难度较难

已知以点C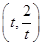(t∈R，t≠0)为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为原点．
(1)求证：△AOB的面积为定值；
(2)设直线2x＋y－4＝0与圆C交于点M，N，若|OM|＝|ON|，求圆C的方程；
(3)在(2)的条件下，设P，Q分别是直线l：x＋y＋2＝0和圆C上的动点，求|PB|＋|PQ|的最小值及此时点P的坐标．

在平面直角坐标系xOy中，曲线y＝x²－6x＋1与坐标轴的交点都在圆C上．
(1)求圆C的方程；
(2)若圆C与直线x－y＋a＝0交于A，B两点，且OA⊥OB，求a的值．

已知点A(－3,0)，B(3,0)，动点P满足|PA|＝2|PB|.
(1)若点P的轨迹为曲线C，求此曲线的方程；
(2)若点Q在直线l₁：x＋y＋3＝0上，直线l₂经过点Q且与曲线C只有一个公共点M，求|QM|的最小值．

如图，四棱柱ABCD－A₁B₁C₁D₁中，侧棱A₁A⊥底面ABCD，AB∥DC，AB⊥AD，AD＝CD＝1，AA₁＝AB＝2，E为棱AA₁的中点．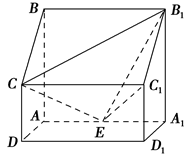

(1)证明B₁C₁⊥CE；
(2)求二面角B₁-CE-C₁的正弦值；
(3)设点M在线段C₁E上，且直线AM与平面ADD₁A₁所成角的正弦值为，求线段AM的长．

在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，且PA⊥平面ABCD.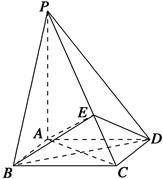

(1)求证：PC⊥BD；
(2)过直线BD且垂直于直线PC的平面交PC于点E，且三棱锥E-BCD的体积取到最大值．
①求此时四棱锥E-ABCD的高；
②求二面角A-DE-B的正弦值的大小．

试卷网试题网古诗词网作文网范文网