如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使平面PDC⊥平面ABCD(如图②)
(Ⅰ)求证AP∥平面EFG;
(Ⅱ)求二面角G-EF-D的大小;
(Ⅲ)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证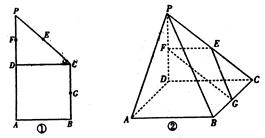 明.
明.
已知定圆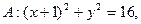 圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
(I)求曲线C的方程;
(II)若点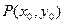 为曲线C上一点,求证:直线
为曲线C上一点,求证:直线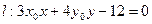 与曲线C有且只有一个交点.
与曲线C有且只有一个交点.
已知抛物线 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(I)求抛物线C的焦点坐标;
(II)若点M满足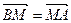 ,求点M的轨迹方程.
,求点M的轨迹方程.
已知椭圆W的中心在原点,焦点在 轴上,离心率为
轴上,离心率为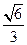 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为 ,过左准线与
,过左准线与 轴的交点
轴的交点 任作一条斜率不为零的直线
任作一条斜率不为零的直线 与椭圆W交于不同的两点
与椭圆W交于不同的两点 、
、 ,点
,点 关于
关于 轴的对称点为
轴的对称点为 .
.
(Ⅰ)求椭圆W的方程;
(Ⅱ)求证: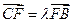 (
(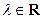 );
);
(Ⅲ)求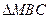 面积
面积 的最大值.
的最大值.
已知圆 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足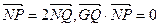 .
.
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线 ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设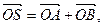 是否存在这样的直线
是否存在这样的直线 ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
已知线段AB过 轴上一点
轴上一点 ,斜率为
,斜率为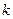 ,两端点A,B到
,两端点A,B到 轴距离之差为
轴距离之差为
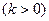 ,
,
(1)求以O为顶点, 轴为对称轴,且过A,B两点的抛物线方程;
轴为对称轴,且过A,B两点的抛物线方程;
(2)设Q为抛物线准线上任意一点,过Q作抛物线的两条切线,切点分别为M,N,求证:直线MN过一定点;