(满分14分)已知函数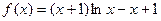 .
.
(1)若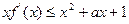 ,求a的取值范围;
,求a的取值范围;
(2)证明: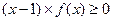 .
.
(本小题满分14分)
一个几何体是由圆柱 和三棱锥
和三棱锥 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中 ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求二面角 的平面角的大小.
的平面角的大小.
(本小题满分12分)
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
 |
|
| 偏高 |
2 |
 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为 .
.
(1)试确定 、
、 的值;
的值;
(2)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(3)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
(本小题满分12分)
如图2,渔船甲位于岛屿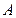 的南偏西
的南偏西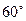 方向的
方向的 处,且与岛屿
处,且与岛屿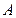 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿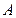 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度;
(2)求 的值.
的值.
设函数 处的切线与直线
处的切线与直线 平行.
平行.
(1)求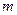 的值;
的值;
(2)求函数 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若 ,根据上述(I)
,根据上述(I) 、(II)的结论,证明:
、(II)的结论,证明:
(1)已知 是正常数,
是正常数, ,
, ,求证:
,求证: ,指出等号成立的条件;
,指出等号成立的条件;
(2)利用(1)的结论求函数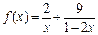 (
(
 )的最小值,并指出取最小值时
)的最小值,并指出取最小值时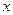 的值.
的值.