已知定义在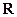 上的函数
上的函数 满足:
满足: ,且对于任意实数
,且对于任意实数 ,总有
,总有 成立.
成立.
(1)求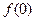 的值,并证明函数
的值,并证明函数 为偶函数;
为偶函数;
(2)若数列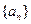 满足
满足 ,求证:数列
,求证:数列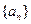 为等比数列;
为等比数列;
(3)若对于任意非零实数 ,总有
,总有 .设有理数
.设有理数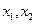 满足
满足 ,判断
,判断 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日期 |
4月1日 |
4月7日 |
4月15日 |
4月21日 |
4月30日 |
温差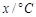 |
10 |
11 |
13 |
12 |
8 |
发芽数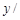 颗 颗 |
23 |
25 |
30 |
26 |
16 |
(Ⅰ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出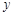 关于
关于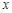 的线性回归方程
的线性回归方程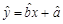 ;
;
(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅰ)中所得的线性回归方程是否可靠?
(参考公式: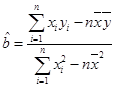
 ,
,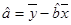 )
)
(参考数据: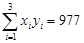 ,
,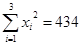 )
)
已知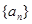 为等差数列,且
为等差数列,且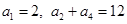 ,
,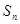 为
为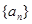 的前
的前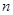 项和.
项和.
(Ⅰ)求数列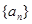 的通项公式
的通项公式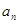 及
及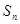 ;
;
(II)设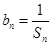 ,求数列
,求数列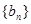 的通项公式
的通项公式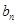 及其前
及其前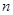 项和
项和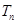 .
.
在平面直角坐标系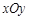 中,动点
中,动点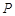 到两点
到两点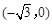 ,
,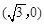 的距离之和等于4,设点
的距离之和等于4,设点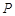 的轨迹为曲线C,直线过点
的轨迹为曲线C,直线过点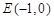 且与曲线C交于A,B两点.
且与曲线C交于A,B两点.
(Ⅰ)求曲线C的轨迹方程;
(Ⅱ)是否存在△AOB面积的最大值,若存在,求出△AOB的面积;若不存在,请说明理由.
已知经过点A(-4,0)的动直线l与抛物线G: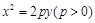 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是 时,
时, .
.
(Ⅰ)求抛物线G的方程;
(Ⅱ)设线段BC的垂直平分线在y轴上的截距为b,求b的取值范围.
已知双曲线 (a>0,b>0)的离心率
(a>0,b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离是
,过点A(0,-b)和B(a,0)的直线与原点的距离是 .
.
(Ⅰ)求双曲线的方程及渐近线方程;
(Ⅱ)若直线y=kx+5 (k≠0)与双曲线交于不同的两点C、D,且两点都在以A为圆心的同一个圆上,求k的值.