(本小题满分10分)
已知函数f(x)= m·log2x + t的图象经过点A(4,1)、点B(16,3)及点C(Sn,n),其中Sn为数列{an}的前n项和,n∈N*.
(Ⅰ)求Sn和an;
(Ⅱ)设数列{bn}的前n项和为Tn , bn = f(an) – 1, 求不等式Tn£ bn的解集,n∈N*.
已知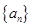 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项 ,
,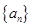 的部分项
的部分项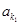 、
、 、…、
、…、 恰为等比数列,且
恰为等比数列,且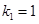 ,
,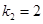 ,
,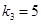 .
.
(1)求数列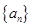 的通项公式
的通项公式 (用
(用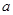 表示);
表示);
(2)若数列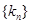 的前
的前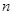 项和为
项和为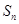 ,求
,求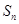 .
.
已知函数 .
.
(1)当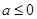 时,求函数
时,求函数 单调区间;
单调区间;
(2)若函数 在区间[1,2]上的最小值为
在区间[1,2]上的最小值为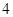 ,求
,求 的值.
的值.
如图所示的多面体中,  是菱形,
是菱形, 是矩形,
是矩形, 面
面 ,
,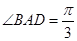 .
.
(1)求证:平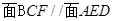 ;
;
(2)若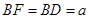 ,求四棱锥
,求四棱锥 的体积.
的体积.
如图,在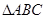 中,
中, ,
, ,
,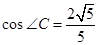 ,点
,点 是
是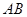 的中点.
的中点.
(1)求边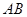 的长;
的长;
(2)求 的值和中线
的值和中线 的长
的长
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是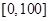 ,样本数据分组为
,样本数据分组为 ,
, ,
,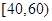 ,
,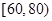 ,
, .
.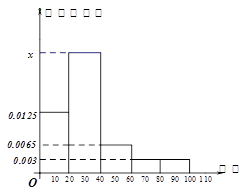
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿.