已知函数
．
（1）当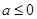
时，求函数
单调区间；
（2）若函数在区间[1,2]上的最小值为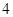
,求
的值．
已知数列{bn}是等差数列，b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+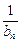
)(其中a＞0且a≠1)记Sn是数列{an}的前n项和，试比较Sn与
logabn+1的大小，并证明你的结论
设实数q满足|q|＜1,数列{an}满足：a1=2,a2≠0,an·an+1=－qn,求an表达式，又如果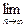
S2n＜3,求q的取值范围
是否存在a、b、c使得等式1·22+2·32+…+n(n+1)2=
(an2+bn+c)
用数学归纳法证明4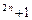
+3n+2能被13整除，其中n∈N*.
设D是△ABC的BC边上一点，把△ACD沿AD折起，使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.
(1)求证：直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°；
(2)若∠BAC=90°，二面角C′—AD—H为60°，求∠BAD的正切值.
