(本题12分)已知向量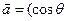 ,
,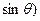 ,
,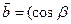 ,
,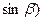 ,且
,且 与
与 之间有关系式:
之间有关系式: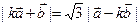 ,其中k>0.
,其中k>0.
(1) 试用k表示 ;(2)求
;(2)求 的最小值,并求此时
的最小值,并求此时 与
与 的夹角
的夹角 的值.
的值.
(本题14分)已知点(1, )是函数
)是函数 且
且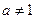 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列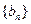
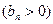 的首项为
的首项为 ,且前
,且前 项和
项和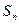 满足
满足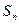 -
- =
= +
+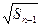 (
( ).
).
(1)求数列 和
和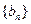 的通项公式;
的通项公式;
(2)若数列{ 前
前 项和为
项和为 ,问
,问 的最小正整数
的最小正整数 是多少? .
是多少? .
(本题14分)如图,在四棱锥 中,底面
中,底面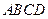 是边长为1的菱形,
是边长为1的菱形, ,
,  ,
, 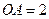 ,
, 为
为 的中点,
的中点, 为
为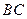 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)求异面直线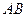 与
与 所成角的大小;
所成角的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.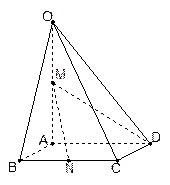
(本题14分)某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养 中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
若(本题12分)在△ABC中, ,
, ,
,  分别为内角A, B, C的对边,且
分别为内角A, B, C的对边,且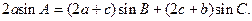
(Ⅰ)求A的大小;(Ⅱ)求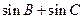 的最大值.
的最大值.
本题12分)已知 且
且 ,命题P:函数
,命题P:函数 在区间
在区间 上为减函数;命题Q:曲线
上为减函数;命题Q:曲线 与
与 轴相交于不同的两点.若“
轴相交于不同的两点.若“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.