某高等学校自愿献血的50位学生的血型分布的情况如下表:
| 血型 |
A |
B |
AB |
O |
| 人数 |
20 |
10 |
5 |
15 |
(1) 从这50位学生中随机选出2人,求这2人血型都为A型的概率;
(2)现有一位血型为A型的病人需要输血,要从血型为A,O的学生中随机选出2人准备献血,记选出A型血的人数为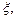 求随机变量
求随机变量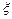 的分布列及数学期
的分布列及数学期 望.
望.
(12分)设函数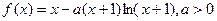 .
.
(1)求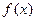 的单调区间;
的单调区间;
(2)证明: .
.
(1 2分)若存在实数
2分)若存在实数 和
和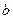 ,使得函数
,使得函数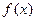 与
与 对其定义域上的任意实数
对其定义域上的任意实数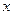 分别满足
分别满足 :
: ,则称直线
,则称直线 为
为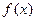 与
与 的“和谐直线”.已知
的“和谐直线”.已知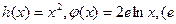 为自然对数的底数);
为自然对数的底数);
(1)求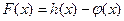 的极值;
的极值;
(2)函数 是否存在和谐直线?若存在,求出此和谐直线方程;若不存在,请说明理由.
是否存在和谐直线?若存在,求出此和谐直线方程;若不存在,请说明理由.
已知函数 满足
满足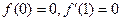 ,且
,且 在
在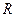 上单调递增.
上单调递增.
(1)求 的解析式;
的解析式;
(2)若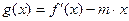 在区间
在区间 上的最小值为
上的最小值为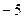 ,求实数
,求实数 的值.
的值.
已知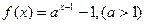 的反函数为
的反函数为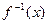 .
.
(1)若函数 在区间
在区间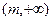 上单增,求实数
上单增,求实数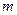 的取值范围;
的取值范围;
(2)若关于 的方程
的方程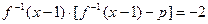 在
在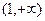 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数 的取值范围.
的取值范围.
已知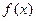 是定义在
是定义在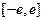 上的奇函数,当
上的奇函数,当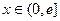 时,
时,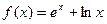 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(1)求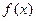 的解析式;
的解析式;
(2)求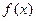 的图象在点
的图象在点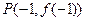 处的切线方程.
处的切线方程.