若f(x)是定义在(0,+∞)上的增函数,且对一切x>0满足
(1)求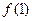 的值;
的值;
(2)若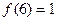 ,解不等式
,解不等式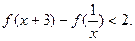
直线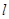 过点P(0,2)且与椭圆
过点P(0,2)且与椭圆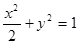 相交于M,N两点,求
相交于M,N两点,求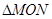 面积的最大值。
面积的最大值。
已知抛物线 与直线
与直线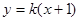 相交于A,B两点。
相交于A,B两点。
(1)求证:OA⊥OB;
(2)当 的面积等于
的面积等于 时,求
时,求 的值。
的值。
椭圆E: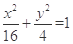 内有一点P(2,1),求经过P并且以P为中点的弦所在直线方程.
内有一点P(2,1),求经过P并且以P为中点的弦所在直线方程.
(本小题满分14分)某房地产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
(Ⅰ)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(Ⅱ)若干年后开发商为了投资其他项目,有两种处理方案:①年平均利润最大时以46万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多?
(本小题满分14分)设数列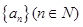 满足
满足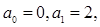 且对一切
且对一切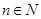 ,有
,有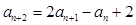 .
.
(1)求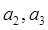 的值;
的值;
(2)证明:数列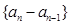 为等差数列;
为等差数列;
(3)求数列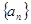 的通项公式;
的通项公式;
(4)设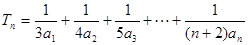 ,求证:
,求证: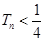 .
.