(本小题满分12分)如图,在四棱锥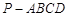 中,
中, 平面
平面 ,
, ,且
,且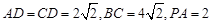 ,点
,点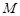 在
在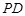 上.
上.
(1)求证: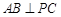 ;
;
(2)若二面角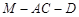 的大小为
的大小为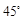 ,求
,求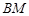 与平面
与平面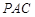 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)在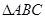 中,角
中,角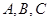 所对的边分别为
所对的边分别为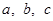 ,满足
,满足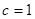 ,且
,且 .
.
(1)求C的大小;
(2)求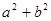 的最大值,并求取得最大值时角A,B的值.
的最大值,并求取得最大值时角A,B的值.
(本小题满分12分)退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构
为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600
人进行调查,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]绘制频率分布直方
图,如图所示.若规定年龄分布在[20,40)岁的人为“青年人”,[40,60)为“中年人”, [60,80]为“老年人”.
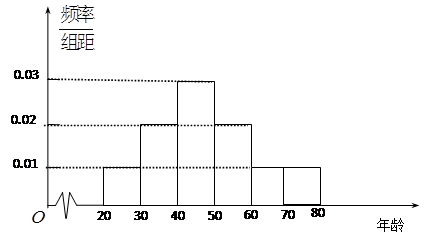 |
(1)若每一组数据的平均值用该区间中点值来代替,试估算所调查的600人的平均年龄;
(2)将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率.从该城市20-80年龄段市民中
随机抽取3人,记抽到“老年人”的人数为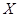 ,求随机变量
,求随机变量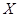 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)已知椭圆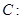
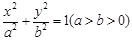 的右焦点为
的右焦点为 ,且点
,且点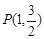 在椭圆
在椭圆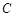 上,
上,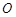 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆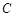 的标准方程;
的标准方程;
(Ⅱ)设过定点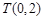 的直线
的直线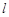 与椭圆
与椭圆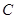 交于不同的两点
交于不同的两点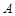 、
、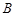 ,且
,且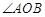 为锐角,求直线
为锐角,求直线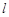 的斜率
的斜率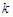 的取值范围;
的取值范围;
(Ⅲ)过椭圆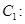
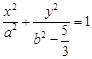 上异于其顶点的任一点
上异于其顶点的任一点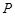 ,作圆
,作圆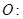
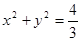 的两条切线,切点分别为
的两条切线,切点分别为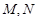 (
(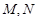 不在坐标轴上),若直线
不在坐标轴上),若直线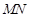 在
在 轴、
轴、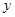 轴上的截距分别为
轴上的截距分别为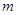 、
、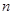 ,证明:
,证明: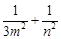 为定值.
为定值.
(本小题满分14分)已知函数 ,(其中常数
,(其中常数 )
)
(Ⅰ)当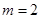 时,求
时,求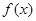 的极大值;
的极大值;
(Ⅱ)试讨论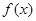 在区间
在区间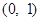 上的单调性;
上的单调性;
(Ⅲ)当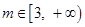 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点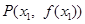 、
、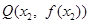 ,使得曲线
,使得曲线 在点
在点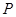 、
、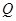 处的切线互相平行,求
处的切线互相平行,求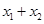 的取值范围.
的取值范围.