如图，在三棱拄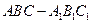
中，
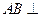侧面
，
已知
（Ⅰ）试在棱
(不包含端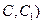点
上确定一点
的位置,使得
；
(Ⅱ) 在（Ⅰ）的条件下,求二面角
的平面角的正切值.
设函数
(1)求不等式
的解集；
(2)若不等式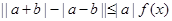
（
，
，
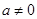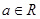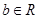）恒成立，求实数
的范围．
已知圆的极坐标方程为ρ2－4
ρ·cos
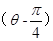＋6＝0.
(1)将极坐标方程化为普通方程，并选择恰当的参数写出它的参数方程；
(2)若点P(x，y)在该圆上，求x＋y的最大值和最小值．
如图，在Rt△ABC中，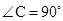
, BE平分∠ABC交AC于点E， 点D在AB上，
．
（1）求证：AC是△BDE的外接圆的切线；
（2）若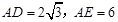
，求EC的长．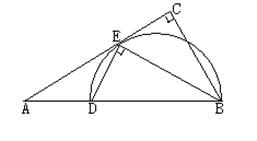
已知
．
.
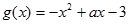（1）求函数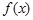
在区间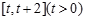
上的最小值；
（2）对一切实数
，
恒成立，求实数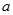
的取值范围；
(3) 证明对一切， 
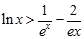恒成立．
实验北校举行运动会，组委会招墓了16名男志愿者和14名女志愿者，调查发现，男、女志愿者中分别有10 人和6人喜爱运动，其余不喜爱.
（1）根据以上数据完成以下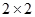
列联表：
（2）根据列联表的独立性检验，有多大的把握认为性别与喜爱运动有关？
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人，求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率．
参考公式 ：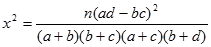
（其中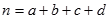
）
 |
 |
 |
 |
|
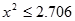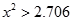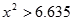| 是否有关联 |
没有关联 |
90% |
95% |
99% |